Compound Annual Growth Rate - Explained
What is a Compound Annual Growth Rate?
- Marketing, Advertising, Sales & PR
- Accounting, Taxation, and Reporting
- Professionalism & Career Development
-
Law, Transactions, & Risk Management
Government, Legal System, Administrative Law, & Constitutional Law Legal Disputes - Civil & Criminal Law Agency Law HR, Employment, Labor, & Discrimination Business Entities, Corporate Governance & Ownership Business Transactions, Antitrust, & Securities Law Real Estate, Personal, & Intellectual Property Commercial Law: Contract, Payments, Security Interests, & Bankruptcy Consumer Protection Insurance & Risk Management Immigration Law Environmental Protection Law Inheritance, Estates, and Trusts
- Business Management & Operations
- Economics, Finance, & Analytics
- Courses
What is a Compound Annual Growth Rate?
The compound annual growth rate (CAGR) is a measurement of growth of an investment over a multiple periods of time in an investment's lifespan. CAGR is the rate of return of an investment from its initial value to end value if it is compounded over time. That is, the rate at which an investment is expected to from its beginning balance to its ending balance if its profits are reinvested at the end of each year.
How to Calculate Compound Annual Growth Rate
The formula for calculating CAGR is;
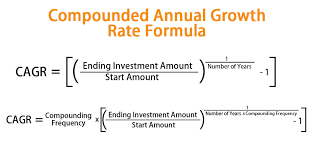
CAGR is calculated by dividing that end value of an investment by its initial value which is raise to an exponent of one, divided by number of years, then remove one from succeeding result.
How is the Compound Annual Growth Rate Used?
The compound annual growth rate (CAGR) measures the rate at which an investment would have grown after a period of years, if it grows at the same rate every year and the returns (profits realized) are reinvested at the end of each year. CAGR aids an easier of understanding of returns when compared to alternative investments. The return rate of an investment is the profit an investment which comprises of change in value and cash flows that an investor receives. Interest and dividends are examples of rate of return on investment. The compound annual growth rate (CAGR) is just a representation of return and not a true return rate.
Compound Annual Growth Rate Example
CAGR is used to smooth returns in terms of investment performance. Highlighted below is an instance of Compound Annual Growth Rate (CAGR); If an investor put in a sum of $10,000 as an investment on March 5, 2005 and by March 5, 2006, the investment grows to $13,000 with a return of $3,000. If by 2007, the investment yields return and increases to $14,000 and by 2008, it grows to $19,500, if arithmetic mean is used in calculating the average annual return for the investment period, the return would be 25.67%. However, using the CAGR formula, the CAGR for this period would be 24.95%, ignoring the difference between the return of some years. CAGR has a number of usefulness, it helps investors forecast future values of investments and also compare a specific investment to alternative investments. CAGR calculates the average growth of a single investment for a period of years. It also helps to smooth returns when growth rates are expected to be volatile and inconsistent, especially in cases of market vulnerability when investment returns become unstable and even. Furthermore, when there is an uneven growth in investment returns, investors apply CAGR in the comparison of two investments so as to understand difference in returns. CAGR track and compare the performance of various businesses. Although, CAGR may look easy to calculate or understand in theory but its practice of application in the real world requires a lot effort, it can be demanding. For instance, if an investor wants to calculate the CAGR of an investment which had a value of $10,000 at the beginning of the investment but was later sold at $16,897.14 after five years, 3 months of investment, the fractional remainder of the holding period must be known. The holding period of an investment is the period between the purchase and sale of a security or the amount of time that the investors hold the investment.
Limitations of Compound Annual Growth Rate - CAGR
Despite the many benefits of uses of the Compound Annual Growth Rate, it has certain limitations. The major clampdown of CAGR is that it neglects the effects market vulnerability in the growth of investments. It always assume that the growth is steady over a period of time, only the smoothed rate of growth is calculated by CAGR. Also, the result of CAGR is unlike to predict the perfect future growth of an investment, its results can rarely serve as historical results. This is because the evaluation might omit vital information about the history of a fund. Another limitation of CAGR the result of provides is a representational figure and not a true return rate. CAGR has transcended from its original function into serving other functions. The CAGR formula can be manipulated algebraically to evaluate the present and future value of money. By calculating the average return that an investment would yield over a period of time (especially long-term investment), an investor can have an idea of the returns of profits realizable in the future. For instance, an investor who wants to establish a private company in 20 years time which will require about $100,000 can decide to invest an amount upon calculating the returns of the investment in 20 years time. This manipulation helps investors discover how much they need to invest at a present time to realize the amount they need in future time. Generally, CAGR is a method used by investors to measure their investment performance in relation to investment returns or profit. It evaluates the rate of return realizable if annual profits made on investments are reinvested. CAGR does this calculation without considering market volatility and how it affects market returns. CAGR presents the overall growth of investment over a period of time if the annual returns are invested again each year.